How to Describe a Normal Distribution
This is also known as a z distribution. In a normal distribution the mean is zero and the standard deviation is 1.
Normal Distributions Review Article Khan Academy
A standard normal distribution has a mean of 0 and variance of 1.
. The normal distribution is a continuous probability distribution that is symmetrical around its mean most of the observations cluster around the central peak and the probabilities for values further away from the mean taper off equally in both directions. Note the classical bell-shaped symmetric histogram with most of the frequency counts bunched in the middle and with the counts dying off out in the tails. If our variable follows a normal distribution the quantiles of our variable must be perfectly in line with the theoretical normal quantiles.
Bell shaped Symmetrical Unimodal it has one peak Mean and median are equal. Bell-Shaped A histogram is bell-shaped if it resembles a bell curve and has one single peak in the middle of the distribution. A Z distribution may be described as N 0 1.
The most common real-life example of this type of distribution is the normal distribution. All forms of normal distribution share the following characteristics. The mean and the.
The mean median and mode are exactly the same. The Box-Cox transformation and the. Mean median mode symmetry about the center 50 of values less than the mean and 50 greater than the mean Quincunx You can see a normal distribution being created by random chance.
Normal left uniform middle and exponential right QQ Plots. Hence a curve is regarded as skewed if it is shifted towards the right or the left. In a normal distribution the mean mean and mode are equalie Mean Median Mode.
The symmetric shape occurs when one-half of the observations fall on each side of the curve. This means that the distribution curve can be divided in the middle to produce two equal halves. If x is two standard deviations above its mean x equals the mean 5 plus 2 times the standard deviation 12.
A straight line on the QQ Plot tells us we have a normal distribution. The Normal Distribution has. The normally distributed curve should be symmetric at the centre.
The Z- distribution also called the standard normal distribution has a. Uniform A histogram is described as uniform if every value in a dataset occurs roughly the same number of times. Skewed Distributions We call distributions that are not symmetrical skewed.
Share Improve this answer. They are represented by a bell curve. The value of X where this occurs is the one thats two standard deviations above its mean.
The center of the distribution is easy to locate and both tails of the distribution are the approximately the same length. The normal distribution is a continuous probability distribution that is symmetrical on both sides of the mean so the right side of the center is a mirror image of the left side. The intersection is 6772.
The first distribution is unimodal it has one mode roughly at 10 around which the observations are concentrated. Have a play with it. In economics distribution is the way total output income or wealth is distributed among individuals or among the factors of production such as labour land and capital.
Normal distributions have key characteristics that are easy to spot in graphs. A normal distribution is the proper term for a probability bell curve. In general theory and in for example the US.
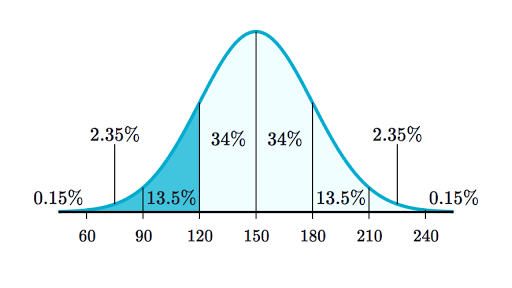
Normal distributions are symmetrical but not all symmetrical distributions are normal. A normal distribution is without any skewness as it is symmetrical on both sides. 68 of the data is within 1 standard deviation σ of the mean μ 95 of the data is within 2 standard deviations σ of the mean μ and 997 of the data is within 3 standard deviations σ of the mean μ.
From a physical scienceengineering point of view the normal distribution is that distribution which. You may see the notation N μ σ 2 where N signifies that the distribution is normal μ is the mean and σ 2 is the variance. Note that all three distributions are symmetric but are different in their modality peakedness.
The second distribution is bimodal it has. Extreme values in both tails of the distribution are similarly unlikely. In normal distributions the mean median and mode will all fall in the same location.
The normal distribution is commonly associated with the 68-95-997 rule which you can see in the image above. The p-value is less than 0005 which indicates that we can reject the null hypothesis that these data follow the normal distribution. They have a peak in the middle that tapers towards each edge.
Both are located at the center of the distribution About 68 of data falls within one standard deviation of the mean. How do you describe a normal distribution. It is called the Quincunx and it is an amazing machine.
The distribution is symmetric about the meanhalf the values fall below the mean and half above the mean. A lot of things follow this distribution like your height weight and IQ. As we expected the Normal distribution does not fit the data.
The normal distribution is a way of describing the errors that arise when you average up millions of unmeasured sources of variation in the thing you are trying to measure. National Income and Product Accounts each unit of output corresponds to a unit of income. It has the following properties.
The area under the normal distribution curve represents probability and the total area under the curve sums to one. It is symmetric A normal distribution comes with a perfectly symmetrical shape. What are the mean and standard deviation of the Z- distribution.
So what are normal distributions. The distribution can be described by two values. Summary Skewness measures the deviation of a random variables given distribution from the normal distribution which is symmetrical on both sides.
Look in the z-table for the given z-value by finding the intersection. If the distribution is symmetrical but has more than one peak the mean and median will be the same as each other but the mode will be different and there will be more than one. One heuristic explanation of the central limit theorem is a good rationale for the normal distribution being a part of the pedagogy of statistics.
It has zero skew and a kurtosis of 3. The above is a histogram of the ZARR13DAT data set. The total area under the curve should be equal to 1.
X 5 212 74. The normal distribution is the most commonly-used probability distribution in all of statistics. Some of the important properties of the normal distribution are listed below.
This distribution is exciting because its symmetric which makes it easy to work with. Today were interested in normal distributions. For example if you are asked to find the area in the tail to the left of z -046 look up 046 The table below illustrates the result for 046 04 in the left hand colum and 006 in the top row.
Normal Distribution Examples Formulas Uses
Normal Distributions Review Article Khan Academy
Key Properties Of The Normal Distribution Cfa Level 1 Analystprep

0 Response to "How to Describe a Normal Distribution"
Post a Comment